Física II

FÍSICA II


PROPIEDADES FÍSICAS DE LOS FLUIDOS



Se denomina fluidos a los estados de la materia que pueden fluir, es decir, pasar a través de un
orificio.
Los fluidos pueden ser líquidos y gases, ya que ninguno de los dos puede conservar una forma
estable.

No obstante, la diferencia entre ellos es que los primeros se adaptan a la forma del contenedor

que los aloja, mientras que los segundos tienen menor atracción entre sus partículas,

por lo que pueden ser comprimidos, careciendo tanto de volumen como de forma.

Ejemplos

  • El agua que fluye por un río.
  • El aire que respiramos.
  • El aceite en una freidora.
  • El vapor de agua en una taza de té caliente.
  • El petróleo en un motor de automóvil.


1.COHESIÓN.

Fuerza que mantiene unidas a las moléculas de una misma sustancia, y esta es la razón por la

que si dos gotas de agua se encuentran próximas entre sí.


2.ADHESIÓN.

Se llama adherencia o adhesión a la fuerza que permite la atracción de las moléculas de

sustancias iguales o diferentes cuando entran en contacto y se mantienen juntas gracias a las

fuerzas intermoleculares.

EJEMPLOS DE COHESIÓN Y ADHESIÓN

La cohesión hace que el agua forme gotas, la tensión superficial las mantiene esféricas y la adhesión las mantiene en su sitio (en la hoja de una planta, por ejemplo).

Debido a la adhesión, el agua se pega a una superficie de cristal limpia, el yeso en la pizarra y los materiales adhesivos le permiten pegar sellos en los sobres, pegar porcelana rota y unir chapas de madera a madera contrachapada.


3.TENSION SUPERFICIAL.

Es el resultado de las fuerzas de cohesión entre las partículas de un líquido, en otras palabras, es

la tendencia de la superficie de un líquido a contraerse para lograr el área más pequeña.


EJEMPLO
Insectos sobre el agua: Algunos insectos, como los zapateros o las chinches de agua, pueden caminar sobre la superficie del agua sin hundirse. Esto se debe a la tensión superficial del agua. Las patas de estos insectos apenas rompen la superficie del agua debido a la fuerza de la tensión superficial, lo que les permite flotar y moverse sobre ella.

4.VISCOSIDAD.

Se refiere al rozamiento interno que existe entre las capas de un fluido. En los líquidos, esta

propiedad puede variar por efecto de la temperatura. En los gases, sucede el efecto contrario:

si se incrementa la temperatura aumenta su viscosidad.


EJEMPLO
La miel, al igual que la mostaza y el kétchup, son ejemplos de líquidos viscosos o espesos. 
Es un fluido que producen las abejas a partir del néctar de las flores o excrementos de partes vivas de las plantas. Se puede afirmar que la miel es uno de los fluidos animales más viscosos y a su vez más dulces.
Sin embargo, a veces la miel puede presentar distintos grados de viscosidad debido al procesamiento posterior a su captura. Algunas veces mezclan la miel con azúcar y otros elementos para comercializarla y esto hace que pierda viscosidad.



5.CAPILARIDAD.

Se presenta cuando existe contacto entre un líquido y una pared sólida. El ascenso de líquido

“por sí solo” se debe a la capilaridad, y ocurre porque la fuerza de adhesión entre las moléculas

del líquido y de la pared sólida es mayor que la fuerza de cohesión entre las moléculas de líquido.

EJEMPLO
Al igual que ocurre con los insectos, la tensión superficial que se crea hace que la hoja o algunas flores floten en el agua sin que se hundan, pese a que su peso es mayor que el del agua.



6. COMPRENSIBILIDAD


Sustancia o material es el cambio de volumen que experimenta cuando es sometida a un cambio de presión. Por lo general, el volumen disminuye al aplicar una presión sobre un sistema u objeto, en algunas reacciones químicas puede suceder esto, y en los gases también, ya que, al aumentar la frecuencia de las colisiones, las fuerzas repulsivas van tomando lugar.


EJEMPLOS

  1. Cuando se sumerge en agua una lata llena de aire, la lata disminuye su volumen debido a la presión que el agua ejerce sobre ella.
  2. Los tanques de buceo se llenan de aire comprimido para que pueda entrar una mayor cantidad de aire en un mismo volumen.




6.INCOMPRESIBILIDAD.

La incompresibilidad es una cualidad que se refiere a la incapacidad de un material o sustancia

para ser comprimido o reducido en volumen bajo la acción de una fuerza externa. En otras

palabras, un material incompresible no puede ser comprimido o deformado fácilmente cuando

se le aplica presión.

Esta propiedad es comúnmente observada en líquidos y sólidos, ya que las partículas que los

componen están muy cerca unas de otras y no pueden ser comprimidas sin que se rompan las

fuerzas de atracción entre ellas.



EJEMPLOS
  • Agua: Su densidad y volumen permanecen constantes incluso cuando se aplica presión.
  • Jugo: Similar al agua, no se comprime significativamente.
  • Aceite: Mantiene su densidad y volumen sin cambios bajo presión.


7.DENSIDAD:

Es una magnitud escalar que, en general, se mide en kg/m³ o g/cm³. Mide la cantidad de

materia por volumen determinado de una sustancia, independientemente del tamaño y de la

masa.


Su fórmula es: 

ρ= m/v


EJEMPLOS
  • La densidad del acero es mayor que la del algodón, ya que un kilo de acero ocupa menos volumen que un kilo de algodón.
  • La densidad del agua es mayor que la del vapor de agua, puesto que hay más moléculas en un litro de agua que en un litro de vapor.

Problema. 

¿Cuál es la masa de una esfera hecha de osmio de 15 cm de radio?

Partiendo de la ecuación de la densidad: ρ= m/v

Se despeja la masa como: m = ρ∙V

Hace falta calcular el volumen de la esfera, el cual viene dado por la fórmula:


Siendo r el radio de la esfera. Como la densidad del osmio es 22570 kg/m3, conviene expresar los 15 cm en metros:

r = 15 cm = 15 × 10−2 m

V = (4/3)π×(15 × 10−2 m)3 = 0.01414 m3


Este valor se sustituye en el despeje de la masa:

m = ρ∙V = 22570 kg/m3 × 0.01414 m3 = 319.1 kg



8.PESO ESPECÍFICO:

Es la razón entre el peso de una cantidad de una sustancia y su volumen, medida según el

Sistema Internacional en Newtons por metro cúbico (N//m³).

Su fórmula es:

γ= W/v = mg/v = pg


Problema. 

Calcula el peso de un cilindro de aluminio de 5 cm de radio y 4 dm de altura. El peso específico del aluminio es de 2,7
Debemos recordar la fórmula de calculo para el volumen de un cilindro.

V = ∏ x r² x h

Donde:
r = radio
h = altura.
V = 3,14 x 25 cm² x 40 cm

Los 4 dm pasados a cm dan 40 cm y 5 cm elevados al cuadrado dan como resultado 25 cm².

V = 3140 cm³.

Ahora podemos calcular el peso a partir de la fórmula de peso específico.

Peso = Pe x V

Peso = 2,7 g/cm³ x 3140 cm³

Las unidades de volumen quedan canceladas y finalmente el peso nos queda en gramos como corresponde.
Resultado:     Peso = 8478 g.



-Para una mejor comprensión sobre el tema "propiedades de los fluidos", te invito a ver el siguiente video:




HIDROSTÁTICA

La hidrostática o la estática de fluidos es el estudió de las propiedades de los fluidos en reposo

en situaciones de equilibrio, esta se basa en las primera y terceras leyes de Newton.



En el siguiente enlace encontrarás más información:
https://www.youtube.com/watch?v=DpcNgW6HEgI&pp=ygUMSElET1JTVEFUSUNB



HIDRÁULICA

Estudia los fluidos y su comportamiento cuando interactúan con otras sustancias, así como sus propiedades y aplicaciones
 
Dos ramas: 
Hidrostática. Fluido, estado de reposo
Hidrodinámica. Movimiento.


En el siguiente enlace encontrarás más información:


PRESIÓN




Las fuerzas que ejerce un fluido sobre el medio que lo rodea vienen caracterizadas por una sola

magnitudla presión en el fluido, la cual se define como la cantidad de fuerza perpendicular aplicada sobre

una superficie.


Problema: 

¿Cuál es la presión ejercida por una fuerza de 120 N que actúa sobre una superficie de 0.040 metros cuadrados?

Solución: Para ello vamos a tomar nuestros datos que el problema nos provee, por ejemplo nos da una fuerza de 120 N, y a su vez un área de 0.040 
En el siguiente enlace, encontrarás más información:


PRINCIPIO DE PASCAL

Ley que establece que la fuerza aplicada en la superficie de un fluido en reposo (es decir, la

velocidad de sus partículas es cero) e incompresible se transmite con la misma intensidad en

todas las direcciones de dicha sustancia; siempre que el recipiente en el que se encuentre no se

deforme.


PROBLEMA

Calcule la magnitud del torque que se debe aplicar para desplazar la masa. Solución: Debemos aplicar el principio de Pascal para resolver este problema:

Debido a que nos interesa la fuerza aplicada en el área 1 para luego relacionarla con el torque,

es a esta a la que vamos a despejar.


En el siguiente enlace, te muestro más información sobre "El principio de Pascal", seguido de un ejercicio:






PRINCIPIO DE ARQUÍMEDES

El principio de Arquímedes es un principio físico que afirma que: «Un cuerpo total o

parcialmente sumergido en un fluido en reposo, recibe un empuje de abajo hacia arriba igual al

peso del volumen del fluido que desaloja».

Esta fuerza recibe el nombre de empuje hidrostático o de Arquímedes, y se mide en newtons

(en el SIU). El principio de Arquímedes se formula así: E =mg= ρf g V Donde E es el empuje ,

ρf es la densidad del fluido, V el «volumen de fluido desplazado» por algún cuerpo sumergido

parcial o totalmente en el mismo, g la aceleración de la gravedad y m la masa, de este modo, el

empuje depende de la densidad del fluido, del volumen del cuerpo y de la gravedad existente en

ese lugar.


PROBLEMA 

Un enorme globo de helio es capaz de sostener en equilibrio (sin subir ni descender) a una persona.
Suponga que el peso de la persona, más la canasta, cuerdas y globo es de 70 kg. ¿Cuál es el volumen de helio necesario para que esto ocurra? ¿Qué tamaño ha de tener el globo?

Solución:
Empuje es producido principalmente por el volumen de helio y que el empuje del resto de los componentes es muy pequeño en comparación con el del helio que ocupa mucho más volumen.

En este caso, se requerirá de un volumen de helio capaz de proporcionar un empuje de 70 kg + el peso del helio.
El empuje es el producto del volumen de helio por la densidad del helio por la aceleración de gravedad. Ese empuje debe compensar el peso del helio más el peso de todo el resto.

Da⋅V⋅g = Da⋅V⋅g + M⋅g

de donde se concluye que V = M / (Da – Dh)

V = 70 kg / (1.25 – 0,18)kg/m^3 = 65.4 m^3

Es decir, se requieren de 65.4 m^3 de helio a presión atmosférica para que haya sustentación.

Si suponemos un globo esférico podemos encontrar el radio del mismo a partir de la relación entre el volumen y el radio de una esfera:

V = (4/3)⋅π⋅R^3

Resultado. 
De donde R = 2,49 m. Es decir se requerirá de un globo de 5 m de diámetro lleno de helio.


En el siguiente enlace te muestro más información sobre "El principio de Arquímedes", seguido de un ejercicio:





HIDRODINÁMICA

La hidrodinámica investiga fundamentalmente a los fluidos incompresibles, es decir, a los

líquidos, pues su densidad prácticamente no varía cuando cambia la presión ejercida sobre ellos.

Cuando un fluido se encuentra en movimiento una capa se resiste al movimiento de otra capa

que se encuentra paralela y adyacente a ella; a esta resistencia se le llama viscosidad.

Para que un fluido como el agua el petróleo o la gasolina fluyan por un tubería desde una fuente de abastecimiento, hasta los lugares de consumo, es necesario utilizar bombas ya que sin ellas las fuerzas que se oponen al desplazamiento entre las distintas capas de fluido lo impedirán.


Puedes encontrar más información en el siguiente video:




GASTO


Volumen de fluido que se atraviesa el arco de la seccion transversal en un segundo

Q=v/t

Q= Gasto en m3/s o cm3/s

v=volumen del fluido en m3 o cm3

t=tiempo en segundos.


PROBLEMA:
¿Cuál es el gasto de un líquido que fluye con una velocidad de 10 m/s por una tubería de 90 cm
de diámetro? Solución: Anotando nuestros datos del problema: v = 10 m/s D = 90cm = 0.9m G = ? La fórmula que utilizaremos, será la siguiente:


Como el área la podemos obtener a partir del diámetro mediante la fórmula del círculo,
entonces: Sustituyendo nuestros datos:
Obtenemos lo que buscábamos, el gasto. Respuesta: El gasto es de 6.36 m³/s




FLUJO


Cantidad de masa en un fluido que atraviesa el área de la sección transversal de un tubo,

por segundo.

F= m/t

F=Flujo en jg/s o gr/s

m=Masa del fluido en kg o gr

t=tiempo en s.


PROBLEMA

¿Cuál es el flujo de una tubería por la que fluyen 3.5 m³ de agua en 40 s? Solución: Datos, pero teniendo en cuenta que, al ser agua, entonces tendremos que considerar su
densidad: V = 3.5 m³ (es el agua que fluye) t = 40 s F = ? ρ(agua) = 1000 kg/m³ La fórmula que usaremos, será la siguiente:

Sustituyendo datos en nuestra fórmula:

Resultado: Por lo que el flujo será de 87.5 kg/s

De acuerdo a los temas anteriormente vistos, te muestro un video sobre "Gasto y Flujo", para
una mejor comprensión de los temas:



ECUACIÓN DE CONTINUIDAD


Fluido imprescindible establece que la masa total de un fluido que circula por un tubo sin

pérdidas ni ganancias, se mantiene  constante. La masa se conserva sin cambios a medida que

el fluido se desplaza. 

v1=v2

A1d1=A2d2

Cómo=vt, tenemos=A1v1t=A2v2t2

A1v1=A1v2

La e. de continuidad nos indica que el gasto es constante, equivale a la expresión

Q1=Q2

PROBLEMA

Se tiene una tubería de sección transversal variable a través de la cual fluye agua. En
determinado punto, el área de la sección transversal es 0.070 m2 y la rapidez del agua es 3.50 m/s.
Calcular:
a) La rapidez del agua en otro punto de la tubería cuya área de sección transversal es 0.105 m2. SOLUCIÓN
Se emplea la ecuación de continuidad, igualando el caudal del primer punto con el caudal del
segundo. El caudal es: Q = A ∙ v Por continuidad: Q1 = Q2 A1 ∙ v1 = A2 ∙ v2 Ahora sustituyen los datos suministrados por el enunciado: A1 = 0.070 m2 v1 = 3.50 m/s A2 = 0.105 m2 v2 =? Y se despeja v2:


b) El volumen de agua que se descarga por un extremo abierto en 1 hora. SOLUCIÓN B Dado que el caudal también es el volumen por unidad de tiempo, se tiene que:


V = Q∙Δt = (A∙v) Δt El caudal Q se puede calcular con los datos del punto 1 o los del punto 2, ya que es el mismo en
ambos puntos: Q = A1 ∙ v1 = 0.070 m2 ∙ 3.50 m/s = 0.245 m3 / s Sabiendo que 1 hora = 3600 s, el volumen de agua descargado es: V = Q∙Δt = (0.245 m3 / s) × (3600 s) = 882 m3 Resultado b. En 1 hora se descargan 882 m3 de agua por la tubería.

Respecto al tema "Ecuación de continuidad", te muestro el siguiente video




PRINCIPIO DE BERNOULLI


Ecuación que nos describe la forma de comportarse que tiene un fluido que se mueve a la larga

de una línea de corriente y que nos dice que en un fluido ideal la energía, permanece constante

en su recorrido.

 


Esta relación entre velocidad y presión tiene numerosas aplicaciones en situaciones
cotidianas.
A continuación, se presentan algunos ejemplos: 1. Vuelo de aviones y aerodinámica:
El principio de Bernoulli es fundamental en la explicación del vuelo de los aviones.
Al moverse a través del aire, las alas generan diferencias de presión que generan la sustentación
necesaria para mantener el avión en el aire. La forma curva de las alas y la velocidad del flujo
de aire contribuyen a la creación de estas diferencias de presión. 2. Funcionamiento de los rociadores de jardín:
Los rociadores de jardín utilizan el principio de Bernoulli para dispersar el agua en forma de
rocío. El agua se mueve a alta velocidad a través de pequeños orificios en el rociador, lo que
disminuye su presión y crea un efecto de pulverización. 3. Funcionamiento de los aerosoles:
Los aerosoles, como los sprays de pintura o desodorantes, también se basan en el principio de
Bernoulli. Al presionar la boquilla del aerosol, se crea una diferencia de presión que permite
que el líquido salga a alta velocidad en forma de finas partículas. 4. Funcionamiento de los sistemas de ventilación:
En los sistemas de ventilación, el principio de Bernoulli se utiliza para crear corrientes de aire y
mejorar la circulación en espacios cerrados. Al crear diferencias de presión entre las áreas de
alta y baja velocidad, se puede lograr un flujo constante de aire.

En el siguiente enlace te muestro más información sobre el "Principio de Bernoulli", seguido de
un ejercicio:





TEOREMA DE TORICELLI

La velocidad que adquiere contiene en un depósito al salir por una perforación, es igual a la

velocidad que adquiere un cuerpo en caída libre soltado desde la superficie libre del fluido. 

v=√ (2gh)

V=Velocidad de salida de un fluido

g= la aceleración de la fuerza de gravedad 9.81m/s2

h=la altura del nivel del líquido sobre el orificio


PROBLEMA
 
Determinar la magnitud de la velocidad con la que sale un líquido por un orificio localizado a una profundidad de 2.6 metros en un tanque de almacenamiento.

Obtener la magnitud de la velocidad
Datos:





a) Obteniendo la magnitud de la velocidad

Si revisamos la fórmula principal del teorema de torricelli, observamos que:




Si sustituimos nuestros datos en la fórmula, de manera directa podremos encontrar el resultado.




Por lo que obtenemos una velocidad de 7.14 m/s

Resultado:



Forma. Figura que posee un cuerpo en su exteriorización, así reconocemos formas rectangulares,

cuadradas, redondas, rectangulares, etcétera, y distintas formas en un mismo cuerpo.


Volumen.

Cantidad de espacio que ocupa un cuerpo a una sustancia. 



Compresibilidad.  Cambio de volumen que experimento cuando es  sometido a un cambio de presión. 



PRESIÓN ABSOLUTA


La presión absoluta es la que se mide en comparación con el vacío absoluto, por lo cual

siempre es una cantidad positiva.

Esto tiene sentido, ya que en el vacío no hay materia alguna que ejerza fuerza, y en

consecuencia no hay presión.


PROBLEMA

Un manómetro se conecta a una cámara,  arrojando una medida de 24 kPa, en un lugar donde la presión atmosférica es de 92 kPa. ¿Cuál es la presión absoluta de la cámara?

Solución
Un kPa equivale a 1000 Pa, pero como ambos datos están en las mismas unidades, se pueden sumar sin problemas y al final hacer una conversión a pascal si se desea.

Utilizando la ecuación: Pab = Patm + Pman y sustituyendo valores queda:
Resultado:   Pab = 92 kPa + 24 kPa = 116 kPa = 116000 Pa



PRESIÓN RELATIVA


En cambio, la presión relativa se mide siempre respecto a otra que se toma como referencia,

siendo la más usual la que ejerce la masa gaseosa que envuelve a la Tierra: nuestra atmósfera,

ya que siempre estamos sujetos a ella.

Por este motivo la mayoría de los instrumentos utilizados para medir presión, llamados

manómetros, están calibrados para que el cero corresponda precisamente a dicha presión

atmosférica.


PROBLEMA 

Un tanque contiene gasolina y glicerina, dos líquidos no miscibles (no se mezclan) a las alturas indicadas. ¿Cuál es la presión manométrica en el fondo del tanque? Se anexan los pesos específicos, denotados con la letra griega γ, de cada fluido:


γgas = 45.3 lb/ft3

γgly = 78.7 lb/ft3

Solución
El peso específico γ de un fluido es el producto de su densidad por la aceleración de gravedad, por lo tanto la ecuación de la presión relativa se puede expresar así:

Prel = γ.y

La presión relativa en el fondo del tanque se debe tanto al peso de la columna de glicerina como el de la gasolina y es independiente de la forma del tanque:

Prel = γgas . yAB + γgly . yBC = (45.3 x 2 + 78.7 x 3) lb/ft2 = 326.7 lb/ft2



PRESIÓN ATMOSFÉRICA

La presión atmosférica se define como la fuerza por unidad de área que ejerce la atmósfera terrestre, utilizándose el pascal como unidad de medida de la presión en el Sistema Internacional de medidas SI, tanto para la presión atmosférica como cualquier otra.

Al emplear instrumentos como un medidor de presión para neumáticos, por ejemplo, lo que en

realidad medimos es la diferencia que existe entre la presión del neumático y la que ejerce la

atmósfera.

Sin embargo, también existen instrumentos para medir la presión absoluta, los barómetros.

Pab = Patm + Pman


PROBLEMA

¿Cuál es la presión ejercida por una fuerza de 140 N que actúa sobre una superficie de 0.030 m²?
Datos: F = 140 N A = 0.030 m² P = ? La fórmula de la presión atmosférica es:

Sustituyendo nuestros datos:

Respuesta: La presión ejercida es de 4666.67 Pa





De acuerdo a los temas "Presión absoluta", "Presión relativa" y "Presión atmosférica", puedes
complementar tu aprendizaje con el siguiente video:


TERMOLOGÍA

Parte de la física que trata de los fenómenos en que intervienen el calor o la temperatura.

TEMPERATURA.

Es la propiedad física que indica que tan caliente o frío se encuentra un cuerpo con respecto a otro. Al suministrar calor a una sustancia, ésta, además de elevar su temperatura, también modifica sus propiedades. 

Cuando dos cuerpos entran en contacto y están a diferente temperatura, después de cierto tiempo, ambos cuerpos se encontrarán a una temperatura, dejarán de tener intercambio de energía y en su momento, alcanzarán el equilibrio térmico.
La temperatura depende del estado de agitación o de movimiento de las moléculas, es decir, la energía cinética promedio de las moléculas de la sustancia.
Las escalas termométricas originales se definen con base a dos temperaturas fáciles de reproducir:
Punto fijo inferior (punto de congelación), es la temperatura en la que el agua y el hielo coexisten en equilibrio térmico a la presión de 1 atm.
Punto fijo superior (punto de ebullición), es la temperatura a la que el agua y el vapor coexisten a la presión de 1 atm.    



CALOR

Transferencia de energía térmica debida a una diferencia de temperatura entre dos cuerpos. Se representa con la letra C, sus unidades de medida son la caloría y la BTU (Unidad térmica Británica) principalmente. Una caloría equivale a 4.1801 J. 
Junto con ella se relaciona el calor específico de sustancias involucradas. 



ESCALAS DE TEMPERATURA.

Los fenómenos relacionados con el equilibrio térmico son estudiados por la Termometría, la cual es una parte de la física que se refiere a la medición de la temperatura de los cuerpos.
Para medir la temperatura utilizamos un instrumento llamado termómetro, el cual tiene integrada una escala graduada. Existen básicamente cuatro escalas de temperatura utilizadas a nivel mundial y las cuales guardan una relación entre sí. Éstas son:

Escalas Fahrenheit y Celsius: Esta escala, llamada en honor de Daniel Fahrenheit (1686-1736), equivale a asignar el valor de 32° T a la temperatura de fusión del agua y 212° F a la ebullición del agua a presión de la atmósfera. Anders Celsius, en la escala diseñada por él, se basó en el punto de fusión del hielo, al que se asignó un valor de 0 grados, y en el punto de ebullición del agua, al que asignó el valor de 100 grados, bajo presión de una atmósfera (760 mm Hg), por lo que su escala quedó dividida en 100 partes, el símbolo C. Ambas escalas están divididas en 100 partes iguales; una división en la escala Celsius equivale a 1.8 divisiones en la escala Fahrenheit. La relación matemática que indica esto es la siguiente: "F=(1.8)(°)+32.
Escala Kelvin:  La escala de temperatura Kelvin está basada en el cero absoluto, En la escala Kelvin, el punto cero (0 K), es el cero absoluto, el punto de congelación del agua (0°C) es de aproximadamente 273 K y el punto de ebullición (100 °C) es de 373 K. Cada intervalo de esta escala se denomina Kelvin.
Escala Rankine: La escala de temperatura Rankine es una escala de temperatura absoluta propuesta en 1859 por William Rankine. Su símbolo es °R. Tiene su punto cero absoluto en -460 °F y los intervalos de grados son idénticos al intervalo de grado Fahrenheit. La relación entre la temperatura en °R y la temperatura correspondiente en °F es °R= °F +460.

PROBLEMA
Si la temperatura interior de un automóvil con sistema de aire acondicionado es de 10 °C, ¿cuál será su temperatura en la escala Fahrenheit?

Datos:
TC= 10°C
T= ¿?°F

Fórmula:
°F (1.8)(°C) + 32

Desarrollo:
°F = (1.8)(10) + 32

Resultado:
T = 50 °F


MECANISMOS DE TRANSFERENCIA DE CALOR

La Calorimetría es la rama de la física que se encarga de estudiar la medida de las cantidades de calor, es decir, la cantidad de energía presente en los procesos térmicos. La unidad de calor apropiada en el sistema internacional es el Joule, se utiliza, con frecuencia la caloría. Una caloría es la cantidad de calor necesaria para elevar la temperatura de 1 g de agua en grados centígrados. V. MTC


En el sistema Inglés, la unidad de medida de la cantidad de calor es la BTU (Unidad Térmica Británica), la cual se define como la cantidad de calor necesaria para elevar la temperatura de una libra de agua en un grado Fahrenheit. La aplicación más usual de esta medida es en los sistemas de aire acondicionado.
La relación entre estas unidades se menciona a continuación:
  • Una Kcal= 3.97 BTU.
  • Una caloría (cal)= 4.18 Joules.
  • Una kilocaloría= 4186 Joules.
  • Una BTU= 778 ft.lb= 0.232 kcal.
El calor puede transferirse de un lugar a otro por:  


CONDUCCIÓN

Ocurre cuando el calor se transfiere o propaga a través de un cuerpo sólido, por colisiones entre las moléculas de la región más caliente de un cuerpo material y las moléculas más frías, sin que estas sufran ninguna traslación en el interior del cuerpo.


R= representación matemática del flujo calor por conducción es:
H= Q/r= KA ∆T/
H= Velocidad de transferencia del color (cal/s).  
Q= Cantidad de calor, (caloría) T= Tiempo de transferencia de calor (s).
A= Sección transversal (área) (m², cm², mm²).
K= Constante de conductividad térmica (BTU in/ft² h °F)
∆T=Diferencia de temperaturas (°C, °F).
/ =Longitud conductor (espesor) (m, cm, mm).

La conductividad térmica es la capacidad que tiene una sustancia para conducir el calor. 
Se representa: K= Q/ AT∆T


CONVECCIÓN

Se presenta cuando la propagación del calor es ocasionada por el movimiento de la sustancia caliente.
Fórmula para calcular el calor transferido por convección:
H= Q/T= hA∆T

Donde:

H= Velocidad de transferencia de calor (cal/s).

Q= Cantidad de calor (caloría).

T= Tiempo de transferencia del calor (s).

h= Coeficiente de convección (kcal/m²,s,°C).

A= Sección transversal (área m², cm², mm²).

∆T= Diferencia de temperaturas en °C o °F.

RADIACIÓN

Es el proceso mediante el cual el calor se transfiere de ondas electromagnéticas esparcidas, originadas a nivel atómico, incluso en el vacío, a una velocidad máxima de 300 000 km/s.
Todo cuerpo caliente irradia calor y cuando este calor llega a otro cuerpo, una parte es absorbida y otra es reflejada.


EMISIVIDAD (e)

Mide la capacidad de un cuerpo para-absorber o emitir radiación térmica, es una cantidad adimensional con un valor numérico que se encuentra ente O y 1, dependiendo de la naturaleza de la superficie. Cuando se tiene un cuerpo negro, la emisividad de éste es de 1. La velocidad de radiación R se define formalmente como la energía radiante emitida por unidad de área por unidad de tiempo, o dicho de otro modo, la potencia por unidad de área.
Si la potencia radiante P, se expresa en watts y la superficie A (área ) en m², la velocidad de radiación estará expresada en watts por m². Como ya la hemas dicho, esta velocidad depende de 2 factores: la temperatura absoluta T y la emisividad (e) del cuerpo radiante. El enunciado formal de esta dependencia, conocida como la ley de Stefan-Boltzmann, se representa:
Er= Pr/A= eσT⁴
Donde:
Er= Energía radiada por unidad de tiempo, por unidad de área. 
P= Potencia radiante, watts.
A = Area, m².
e= Emisividad de la superfice, de O a 1.
σ= Constante de stefan = 567 x 108/wm²K⁴.
T⁴= La cuarta potencia de la temperatura absoluta K⁴. La constante de proporcionalidad σ es una constante universal. Si la potencia radiante se expresa en watts y la superficie en m², σ tiene el valor de 5.6x10-⁸ m² K4.

La emisividad tiene valores de 0 a 1 dependiendo de la naturaleza de la superficie radiante.


DILATACIÓN

Es la variación en las dimensiones que sufre un cuerpo al experimentar una alteración en la temperatura.
Se clasifica en:
  • Dilatación lineal.
  • Dilatación superficial.
  • Dilatación volumétrica.
  • Dilatación onómala del agua.
Dilatación


DILATACIÓN LINEAL

Es el incremento en la dimensión lineal que experimentan los cuerpos sólidos al aumentar sus temperaturas. Esta dilatación se debe a que la elevación de la temperatura produce un aumento en la distancia promedio entre los átomos.
Al incrementar la temperatura de una barra (de T⁰ a Tf) se incrementa proporcionalmente su longitud.
Introduciendo la constante de proporcionalidad (a) denominado coeficiente de dilatación lineal, la ecuación queda:

∆L= aL⁰∆T

Considerando que:

∆/=/f-/⁰ y sustituyendo en la ecuación anterior, obtenemos: 

/f-f0= a /0 ∆T

Despejando/ (/+αΔΤ)

donde:

∆/ variación de la longitud (m, pie).
a = coeficiente de dilatación lineal (°C-1, °F-1).
/= longitud inicial de la barra (m, pie).
∆T = variación de la temperatura (m, pie).

Coeficiente de dilatación lineal (a) es el incremento lineal que experimenta una varilla de determinada sustancia, de longitud igual a la unidad, al elevarse su temperatura un grado centígrado. 
Es un valor específico para cada material, lo que provoca que se dilaten en diferentes proporciones, pues las fuerzas con que se unen los átomos y las moléculas varían de una sustancia a otra. La representación de este coeficiente es la siguiente:



DILATACIÓN SUPERFICIAL.

Es el incremento de área o superficie que experimenta un cuerpo al incrementar la temperatura.
Al variar la temperatura de una placa, su área varía proporcionalmente.

ΔA es proporcional a A⁰, ∆T.

Introduciendo la constante de proporcionalidad (β) la ecuación queda:

ΔΑ= βΑ⁰ΔΤ

Sustituyendo en la ecuación anterior, obtenemos: Αf= Α⁰ (1 + βΔΤ)
donde:
  • ∆A = Variación en el área de la placa (m²).
  • β = Coeficiente de dilatación superficial (°C-1).
  • A¹ = Área inicial de la placa (m²).
  • ∆T = Variación de la temperatura (°C).
  • A² = Área final de la placa (m²).
Coeficiente de dilatación superficial es el incremento en el área que experimenta una placa de determinado material, de superficie igual a la unidad, al elevarse su temperatura un grado centígrado.
Es específico para cada material y no se necesitan tablas, ya que el valor se obtiene multiplicando por dos el coeficiente de dilatación lineal.
β= 2a


CALOR ESPECÍFICO

Una vez que se ha transferido de un cuerpo a otro, ya no se le denomina calor, sino energía interna. Dicha energía de las sustancias se define como la suma de las energías cinética y potencial de todas las moléculas individuales que la constituyen.
Como la energía debe conservarse, entonces el calor cedido por cuerpo caliente es el equivalente al ganado por el cuerpo frío, es decir, calor cedido=calor ganado. Es aquí que la temperatura se entiende como una unidad fundamental para determinar la cantidad de calor cedido. Para calcular la cantidad de calor. Video. CE

Q= mC∆T

donde:
  • C= calor específico (cal/gr°C o BTU/Lb°F)
  • m= masa (gr o lb).
  • Q= cantidad de calor (cal o BTU).
  • ∆T= cambio de temperatura (°C o °F).
Todo cuerpo o sustancia tiene la capacidad de transferir energía a otro cuerpo con temperatura más baja. El calor específico es la cantidad de calor necesaria para elevar en un grado la temperatura de una unidad de masa:
C=Q/m∆T
Algunos calores específicos más comunes a utilizar son los siguientes: 

Problema. En una esfera de metal se encontró que su masa es de 15 g y la cantidad de calor absorbida al aumentar su temperatura en 10 °C es 8.5 cal.
 ¿Cuál es el valor del calor específico?

Datos:
m = 15gr
Q = 8.5cal
∆T = 10  °C

Fórmula:
C= Q/mT

Resultado: 
C= 8.5 Cal/(15g)(10°C).
C= 5.6


SISTEMA TERMODINAMICO

Un sistema es una porción del universo que se toma como objeto de estudio y que separamos del resto del universo por medio de un límite o frontera. El entorno es la parte del universo más próxima al sistema y que se ve afectada de algún modo por los procesos que ocurren dentro del sistema. 
El sistema puede ser: 
  • CERRADO.
Consiste en una región de masa constante; a través de los límites solo se permite la transferencia de energía. Se denomina masa de control. 
  • ABIERTO.
En este es posible la transferencia de masa y de energía a través de sus límites; la masa contenida en él no es constante. La superficie limitante (imaginaria), se llama superficie de control. 
  • AISLADO.
Este no puede transferir materia ni energía con el medio. El universo en su totalidad se considera como un sistema aislado. 


PROCESOS TERMODINAMICOS.

Involucrados con estudiar las dos leyes básicas que deben obedecerse cuando se utiliza energía térmica para realizar trabajo. La termodinámica es la rama de la física que estudia todas las transformaciones de una forma de energía en otra, y también la transmisión o transferencia de determinada clase de energía. Se trata de la relación estrecha que guarda el trabajo y el calor en las sustancias. 


a) Proceso adiabático.
Si el sistema no cede ni recibe calor, por lo que se desarrolla a un calor constante. Se utilizan fronteras hechas con paredes adiabáticas. 

b) Proceso no adiabático.
Cuando el sistema interactúa térmicamente con los alrededores por lo que el calor fluye a través de las paredes diatérmicas que los constituyen. Durante este tipo de procesos térmicos un sistema absorbe o cede calor. La cantidad de calor intercambiado en estos varía según la sustancia y el proceso de que se trate.
En un sistema con pared diatérmica existe interacción del sistema con los alrededores, ya que la pared diatérmica permite la transferencia de calor.
Una pared adiabática no permite que exista interacción térmica del sistema con sus alrededores. 


ENERGÍA INTERNA

Se define como la suma de las cargas cinéticas y potencial de las moléculas individuales que lo constituyen.

Cuanto mayor sea la temperatura de un sistema, mayor será su energía interna. En las moléculas, los valores absolutos no se pueden precisar, sólo se determina la variación que sufre la energía del sistema: 
ΔE= E2-E1.
Donde:
  • ΔE= Variación de la energía interna expresada en Joules. (J)
  • E2= Energía interna final en Joules. (J)
  • E1= Energía interna inicial en Joules. (J)
El trabajo de Joule establece el principio llamado equivalente mecánico del calor, en el que se demuestra que por cada Joule de trabajo se producen 0.2389 calorias y que cuando una caloría de energía térmica se convierte en trabajo se obtienen 4.186 Joules.
                       1 cal= 4.186 J.
                       1 J= 0.2389 Cal.


ENERGÍA TÉRMICA

Grado de energía interna contenida en un sistema termodinámico en equilibrio, (un cuerpo, un conjunto de partículas, una molécula, etc) y que es proporcional a su temperatura absoluta. 

Genera el movimiento interno y aleatorio de las partículas de un cuerpo (equivale a la energía cinética) aumenta o disminuye por transferencia de energía, usualmente bajo la forma de calor o de trabajo.
La temperatura de un sistema y su capacidad de generar un trabajo (movimiento) depende de su energía térmica, puede ser transformada, transmitida o conservada hasta cierto punto, la energía térmica es responsable de los estados de agregación de la materia ya que, a mayores niveles de energía, mayor agitación de partículas constituyentes de la materia y menor posibilidad de que compartan un espacio limitado.


TRABAJO Y TERMODINÁMICA

En un trabajo de expansión producido gracias a la energía interna de las moléculas de gas, la temperatura del sistema disminuye. Si al expandirse un gas el volumen final es mayor a la inicial, el trabajo es positivo, entonces el sistema realizó un trabajo sobre los alrededores.

W=p1(V2−V1)
Donde: 
  • W= trabajo realizado a una presión constante del gas (proceso isobárico) (Joules).
  • p= presión constante del gas N/m².
  • (V2-V1)= variación del volumen en el gas (m³)


LEYES DE LA TERMODINÁMICA


Primera ley de la termodinámica 
El cambio en la energía interna de un sistema es igual a la suma de la energía transferida a través de la frontera del sistema por calor y por trabajo, por lo que la energía no se crea ni se destruye, solo se transforma de un tipo a otro.
Matemáticamente se expresa: 
ΔE=Q-W o  ΔE=Q+W
  • Q= calor que entra o sale del sistema. (cal o joules)
  • ΔE= variación de energía interna. (cal o joules)
  • W= trabajo efectuado por el sistema o trabajo realizado sobre este. (joules o cal)
Segunda ley de la termodinámica. 
Señala que existe un límite en la cantidad de trabajo, el cual es posible obtener a partir de un sistema caliente.
Dos investigadores definen la segunda ley como:
  • R.J.E Celsius: el calor no puede por sí mismo, sin la intervención de un agente externo, pasar de un campo frío a uno más caliente.
  • W.T Kelvin: es imposible construir una máquina térmica que transforma en trabajo todo el calor que se le suministra.Quiere decir que ninguna máquina térmica puede tener una eficiencia del 100%.
Leyes Termodinámica


CALORIMETRÍA

Técnica que determina los cambios del contenido calórico de un sistema, asociados con un proceso químico o físico. Estudia la relación que tiene la energía calorífica asociada a una reacción química. Video

Conductividad térmica

Mide la capacidad de un material para conducir el calor. Los materiales con alta conductividad transmiten el calor fácilmente, mientras que los de baja conductividad lo retienen. 
Matemáticamente se expresa:
                                                         Q=K*A* ΔT/L
  • Q= tasa de transferencia de calor en vatios (W).
  • K= conductividad térmica del material en W (m*k).
  • A= área transversal a través de la cual se transfiere el calor en m².
  • ΔT= diferencia de temperatura entre dos extremos del material en Kelvin (K).
  • L= espesor o longitud del material a través del cual se transfiere el calor en metros (m).
Problema. Una pared de ladrillo de 0.2 m de longitud tiene una conductividad de 0.6 vatios por m/k (w/cm*k)). Si la diferencia de temperatura entre el interior y el exterior de la pared es de 20°C. ¿Cuál es la tasa de transferencia de calor a través de la pared?

Datos:                      Formula:
L= 0.2m                   Q= K*A *ΔT/L
K= 0.6 w 
ΔT= 20°C.

Resultado: Para una pared el área se omite porque el calor se transfiere a través de la longitud de la pared. 
Q= 0.6*20/0.2
Q= 60 vatios.


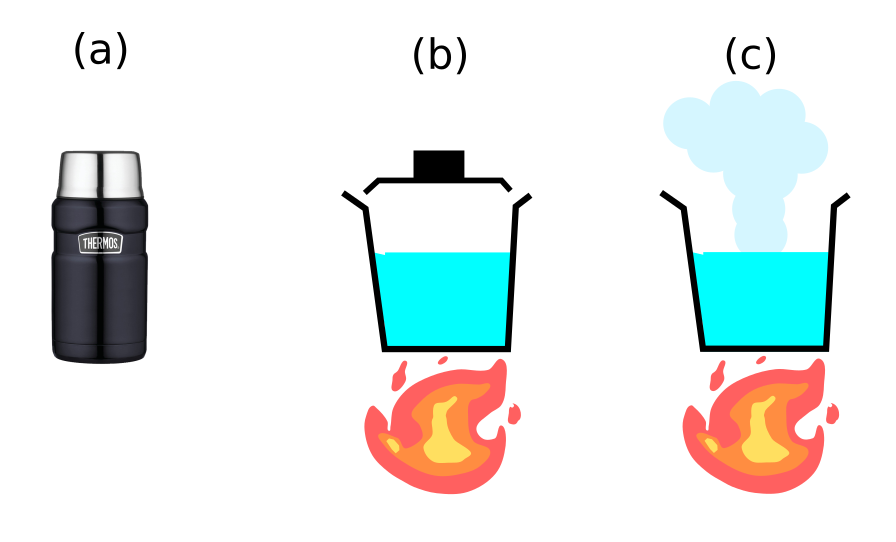
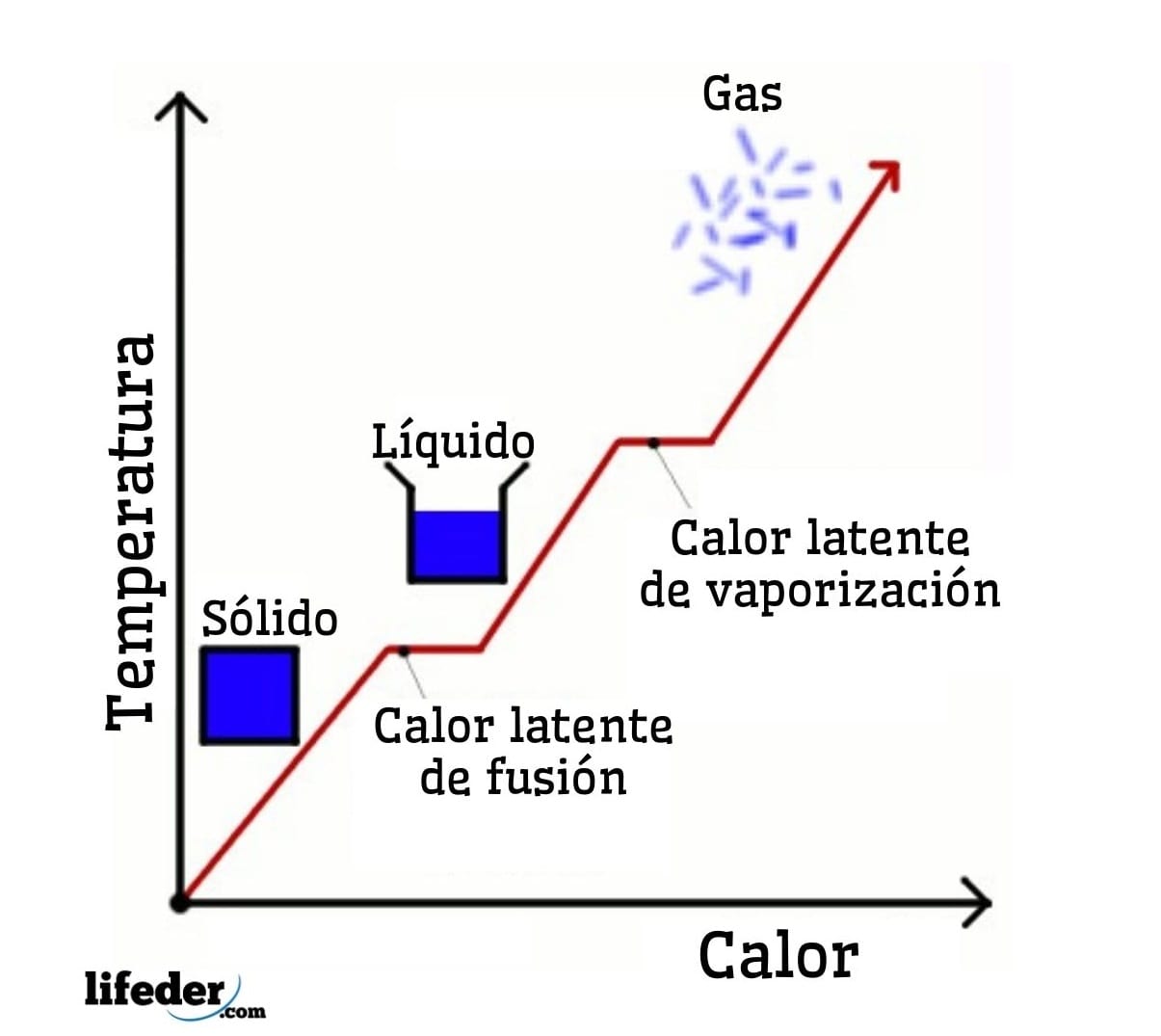
CALOR LATENTE

Tipo de calor que recibe un determinado cuerpo, pero que no produce ningún tipo de incremento en la temperatura del cuerpo, sino que se usa para generar un cambio de estado en la materia. Vídeo
                                                 Q= m*L.
  • Q= calor total o calor total involucrado.
  • m= masa de la sustancia involucrada en el cambio de fase.
  • L= calor latente específico de la sustancia.


  1. Calor latente de fusión. 
Cantidad de calor necesaria para convertir una sustancia de estado sólido a líquido a temperatura constante. 



Problema. ¿Cuánto calor se necesita para fundir 500 g de hielo a 0°C? Sabiendo que el calor latente de fusión del agua es de 334 J/g.

Datos:                   Formula:                 Solución:       
m= 500g.              Q= m*L.                   Q= (500 g)(334 J/g)
L= 334 J/g.                                           Resultado: Q= 167,000 J.
Q= ?

  1. Calor latente de vaporización.
Cantidad de calor necesaria para cambiar una sustancia líquida a la fase gaseosa a temperatura constante. 

Problema. ¿Cuánto calor se necesita para evaporar 200 g de agua a 100°C? Sabiendo que el calor latente de vaporización de agua es de 2260 J/g. 

Datos:                      Formula:             Solución:
m= 200g.                  Q= m*L              Q= (200 g)(2,260 J/g).
L= 2,260 J/g.                                       Resultado: Q= 452,000 J.
Q= ?


ELECTROSTÁTICA

La electrostática es una rama de la Física que estudia los efectos producidos en los cuerpos como consecuencia de sus cargas eléctricas, o lo que es lo mismo, el comportamiento de las cargas eléctricas en situación de equilibrio.
Dicha carga eléctrica es la responsable de los efectos electrostáticos (de atracción o de repulsión) que se generan entre los cuerpos que la poseen. Los primeros indicios del estudio de la electrostática se remontan a la época de los griegos antiguos, cuando el filósofo Tales de Mileto (624 a.C. – 546 a. C.) identificó comportamientos extraños a partir de la fricción del ámbar con tejidos como la lana, generando la atracción de objetos con electricidad estática.


CARGA ELÉCTRICA

La carga eléctrica es una propiedad física fundamental de algunas partículas subatómicas, como electrones y protones. Esta propiedad hace que las partículas experimenten una fuerza cuando están cerca de otras partículas cargadas. Existen dos tipos de cargas eléctricas: positiva y negativa. Cargas
*Carga Positiva: Una carga positiva ocurre cuando un objeto pierde electrones. Las cargas positivas atraen a las cargas negativas.
Ejemplos: Los protones, que se encuentran en el núcleo de los átomos, tienen una carga positiva.
  • Propiedades: Las cargas positivas se repelen entre sí.
*Carga Negativa: Una carga negativa ocurre cuando un objeto gana electrones. Las cargas negativas atraen a las cargas positivas.
Ejemplos: Los electrones, que giran alrededor del núcleo atómico, tienen una carga
negativa.
  • Propiedades: Las cargas negativas se repelen entre sí.

UNIDADES DE MEDIDA

  • La carga eléctrica se representa por la letra q y su unidad en el Sistema Internacional de Unidades es el coulomb cuyo símbolo es la letra C. 
Un coulomb es equivalente a la carga de 6.25 X10'8 electrones, lo cual la hace una unidad demasiado grande para las cantidades de carga que se presentan en muchas situaciones y fenómenos, que son del orden de milicoulomb (mC), microcoulomb (mC) y picocoulomb (pC). Vídeo. UM

Problema:  En una tormenta eléctrica, un rayo transfiere una carga de 100 C de la nube a la superficie terrestre, ¿cuántos electrones se transfirieron de la nube a la Tierra?
Datos
9 =-100C
Se coloca un signo negativo por ser electrones.
e = - 1.6 x 10-19 C
Este es el valor redondeado de e a dos cifras.
n = número de electrones
Fórmula
9 =ne
Al sustituir los valores:
- 100 C = n(-1.6 x 10-19 C)
Resultado.  Despejando n
100 C
n = 1.6 X 10-1 C
n = 62.5 X 1019 electrones


LEY DE CARGAS ELÉCTRICAS

La ley de cargas eléctricas dice que las cargas con el mismo signo se repelen, mientras que las cargas con diferente signo se atraen. Por lo tanto, si tenemos dos cargas positivas o dos cargas negativas, estas se repelen entre sí. Pero si tenemos una carga positiva y una carga negativa, estas se atraen entre sí. La atracción o repulsión de las cargas eléctricas es debido al signo de la fuerza eléctrica resultante. Cuando el signo de las dos cargas es iguales la fuerza eléctrica es positiva, por otro lado, cuando el signo de las cargas es distinto la fuerza eléctrica es negativa. Más abajo veremos cómo se calcula la fuerza eléctrica.
-PRINCIPIO DE CONSERVACIÓN DE LA CARGA
El principio de conservación de la carga es uno de los fundamentos esenciales en física. Según este principio, la cantidad total de carga eléctrica en un sistema aislado permanece constante con el tiempo, independientemente de las interacciones que ocurran entre las partículas dentro del sistema


LA CARGA ESTÁ CUANTIZADA

En la física clásica, se creía que la carga eléctrica podía tomar cualquier valor. Sin embargo, en la física cuántica, se descubrió que la carga está cuantizada.
Esto significa que la carga eléctrica sólo puede existir en múltiplos enteros de una carga elemental. La carga elemental es la cantidad mínima de carga que puede existir


DIFERENTES FORMAS DE ELECTRIZAR UN CUERPO
-CARGA POR FROTAMIENTO: el cuerpo menos conductor saca electrones de las capas exteriores de los átomos del otro cuerpo quedando cargado negativamente y el que pierde electrones queda cargado positivamente.

-CARGA POR CONTACTO: un cuerpo cargado se pone en contacto con otro, la carga eléctrica se distribuye entre los dos y, los dos quedan cargados con el mismo tipo de carga.


Aplicaciones

Proceso de carga de un objeto sin contacto directo. Cuando permitimos que las cargas salgan de un conductor por contacto, decimos que lo estamos poniendo a tierra. 
felicidad-humana-Benjamín Franklin fue el primero en demostrar este  hecho a través de su famoso experimento de la cometa, que le permitió comprobar que los rayos son un efecto eléctrico. Franklin descubrió también que la carga fluye con facilidad hacia o desde objetos puntiagudos y así se construyó el primer pararrayos.


CONDUCTORES Y AISLADORES

Los materiales presentan distintos comportamientos ante el movimiento de cargas eléctricas.
  • Conductores
Los elementos conductores tienen facilidad para permitir el movimiento de cargas y sus átomos se caracterizan por tener muchos electrones libres y aceptarlos o cederlos con facilidad, por lo tanto son materiales que conducen la electricidad.

Ejemplos. 
  1. Cobre.
  2. Aluminio.
  • Aisladores
Los aisladores son materiales que presentan cierta dificultad al paso de la electricidad y al movimiento de cargas. Tienen mayor dificultad para ceder o aceptar electrones. En una u otra medida todo material conduce la electricidad, pero los aisladores lo hacen con mucha mayor dificultad que los elementos conductores.
Ejemplos. 
  1. Plástico 
  2. Cerámica.

LEY DE COULOMB

La ley de Coulomb se emplea en el área de la física para calcular la fuerza eléctrica que actúa entre dos cargas en reposo.
A partir de esta ley se puede predecir cuál será la fuerza electrostática de atracción o repulsión existente entre dos partículas según su carga eléctrica y la distancia que existe entre ambas.
  • La ley de Coulomb debe su nombre al físico francés Charles-Augustin de Coulomb, quien en 1785 enunció esta ley:
“La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario”.
Esta ley constituye la base de la electrostática y se representa de la siguiente manera:
  • F: fuerza eléctrica de atracción o repulsión en Newtons (N). Las cargas iguales se repelen y las cargas opuestas se atraen.
  • k: es la constante de Coulomb o constante eléctrica de proporcionalidad. La fuerza varía según la permitividad eléctrica (ε) del medio, bien sea agua, aire, aceite, vacío, entre otros.
  • q: valor de las cargas eléctricas medidas en Coulomb (C).
  • r: distancia que separa a las cargas y que es medida en metros (m).
Cabe destacar que la permitividad eléctrica del vacío es constante, y una de las más empleadas. Se calcula de la siguiente manera: ε0 = 8,8541878176x10-12 C2 / (N·m2). Es de suma importancia tener en cuenta la permitividad del material.
El valor de la constante de Coulomb en el Sistema Internacional de medidas es:
Valor de la constante de Coulomb en la Ley de Coulomb
Esta ley sólo toma en cuenta la interacción entre dos cargas puntuales al mismo tiempo. Asimismo, sólo determina la fuerza que existe entre q1 y q2, sin considerar las cargas alrededor.
Coulomb logró determinar las propiedades de la fuerza electrostática al desarrollar como instrumento de estudio una balanza de torsión. Esta balanza consiste en una barra que colgaba sobre una fibra con la capacidad de torcerse y volver a su posición inicial.
De esta manera, Coulomb podía medir la fuerza que se ejercía sobre un punto de la barra al colocar varias esferas cargadas a diferentes distancias con el fin de medir la fuerza de atracción o repulsión según girara la barra.

Problema: Tenemos dos cargas eléctricas, una de +3 C y una de -2 C, separadas a una distancia de 3 metros. Para calcular la fuerza que existe entre ambas cargas, es necesario multiplicar la constante K por el producto de ambas cargas. Como se observa en la imagen, se ha obtenido una fuerza negativa.
Ejemplo ilustrado de cómo aplicar la ley de Coulomb:
Problema. Tenemos una carga de 6 x 10-6 C (q1) que se encuentra a 2 metros de distancia de una carga de 4 x 10-6 C (q2). Entonces, ¿cuál es la magnitud de fuerza entre estas dos cargas?
Ejemplo 2 ley de coulomb.1
a. Se multiplican los coeficientes: 9 x 6 x 4= 216. El 9 corresponde al coeficiente de la constante de Coulomb, mientras que el 6 y el 4 corresponden al de las respectivas cargas eléctricas.
b. Se suman de manera algebraica los exponentes: 9 - 6 - 6 = 3. El 9 corresponde al exponente de la constante de Coulomb, mientras que -6 corresponde al de las cargas eléctricas.
Con ello, tenemos:
Ejemplo 2 ley de coulomb.2
Resultado. F = 54 x 10-3 N.


Campo eléctrico 

Un campo eléctrico es un campo físico o región del espacio que interactúa con cargas eléctricas o cuerpos cargados mediante una fuerza eléctrica. Su representación por medio de un modelo describe el modo en que distintos cuerpos y sistemas de naturaleza eléctrica interactúan con él.  Vídeo

Dicho en términos físicos, es un campo vectorial en el cual una carga eléctrica determinada (q) sufre los efectos de una fuerza eléctrica (F).
Estos campos eléctricos pueden ser consecuencia de la presencia de cargas eléctricas, o bien de campos magnéticos variables, como lo demostraron los experimentos de los científicos británicos Michel Faraday y James C. Maxwell.
Por esa razón, los campos eléctricos, en las perspectivas físicas contemporáneas, se consideran junto a los campos magnéticos para formar campos electromagnéticos.
Si esta carga es positiva, genera líneas de campo eléctrico que «nacen» en la carga y se extienden hacia fuera con dirección radial. Si, por el contrario, la carga es negativa, las líneas de campo «mueren» en la carga. Si se acerca una carga a la región del espacio donde existe un campo eléctrico, ésta experimentará una fuerza eléctrica con una dirección y sentido.
La intensidad del campo eléctrico o simplemente campo eléctrico en un punto es una magnitud vectorial que representa la fuerza eléctrica que actúa por unidad de carga testigo positiva, q', situada en dicho punto.
La unidad de intensidad del campo eléctrico en el Sistema Internacional (S.I) es el newton por coulombio (N/C).

Intensidad del Campo creado por una carga puntual

Así, la intensidad del campo eléctrico, o llamada más comúnmente campo eléctrico (de forma simplificada), es un vector que tiene la misma dirección y sentido que la fuerza eléctrica que actúa sobre la carga testigo positiva. Además, su módulo se puede obtener mediante la siguiente expresión:
Tal y como hemos visto anteriormente, en el caso de que deseemos calcular la intensidad del campo eléctrico en un determinado punto creado por una única carga puntual q, deberemos introducir una carga testigo positiva q' en dicho punto. A partir de aquí podemos emplear la ley de Coulomb (para calcular la fuerza electrica que sufre q') y la definición de intensidad del campo en un punto:
Problema. Un ejemplo sencillo del cálculo de la intensidad de un campo eléctrico es: Si introducimos una carga eléctrica de 5×70-6 C en un campo eléctrico que actúa con una fuerza de 0,04 N, ¿con qué intensidad actúa dicho campo? 
Aplicando la fórmula E = F/q, tenemos que E = 0,04 N / 5×10-6 C = 8.000 N/C. La intensidad sería de 8,000 N/C      

Intensidad del Campo creado por varias cargas puntuales

En el caso de que tengamos varias cargas puntuales y deseemos conocer la intensidad del campo eléctrico en un punto podemos hacer uso del principio de superposición:
El campo eléctrico que generan “n” cargas puntuales estáticas en un determinado punto del espacio es la suma vectorial de la intensidad de campo creada por cada una de  las cargas en dicho punto.

Problema. Dadas dos cargas q1=3 µC y q2= 6 µC separadas 2 m. ¿A qué distancia de q2 se encuentra el punto del segmento que une q1 y q2 en el que se anulan los campos eléctricos de ambas cargas?

Datos
 q1=3 µC = 3·10-6 C
 q2= 6 µC = 6·10-6 C
 d = 2 m
Sustituimos valores:

ENERGÍA POTENCIAL ELÉCTRICA

El cambio en la energía potencia, almacenada en q es igual al trabajo que se necesita para llevar q de A a B.
Diferencia en la energía potencial eléctrica.
Como el trabajo, la energía potencial eléctrica es una cantidad escalar.
Ahora hacemos una pequeña manipulación de esta expresión y algo muy especial sucede. Esta línea de razonamiento es similar a nuestro desarrollo del campo eléctrico.

Multiplica los términos
Etiqueta cada término con un nombre para que podamos hablar de ellos por un segundo.  Sea
Vídeo


ENERGÍA POTENCIAL DE UN SISTEMA DE DOS PARTÍCULAS

Si disponemos de dos cargas Q y q, el trabajo para aproximar q desde el infinito hasta un punto A próximo a Q se puede obtener aplicando la definición de trabajo entre dos puntos:
La energía potencial eléctrica que posee una carga puntual q en presencia de otra carga puntual Q que se encuentran separadas cierta distancia r es 

donde:
  • Ep =la energía potencial eléctrica. En el S.I. se mide en Julios (J).
  • Q y q = valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
  • r = valor de la distancia que las separa. En el S.I. se mide en metros (m).
  • K = constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.
Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma:


VOLTAJE

El voltaje es la magnitud responsable de crear la diferencia de potencial eléctrico entre dos puntos, se refiere al trabajo realizado por una unidad de carga eléctrica cuando se desplaza a través de dos puntos en un campo eléctrico específico.  

La medición del voltaje se realiza empleando una herramienta de medición conocida como voltímetro. Este dispositivo se conecta en paralelo con la fuente de energía cuyo potencial eléctrico se desea obtener. Su unidad de medida es el voltio.
Cuando se enuncia en forma explícita, significa que tensión = corriente x resistencia, o voltios = amperios x ohmios, o V = A x Ω
  • Voltaje inducido: fuerza que se induce para generar  la energía eléctrica que recorrerá un circuito.
  • Voltaje alterno: es el más común en las tomas de corriente. Los valores están alternados, su frecuencia varía en función del país donde se ubique.
  • Voltaje de corriente directa: habitual en motores y baterías. Se obtiene al transformar una corriente alterna en una continua.
  • Voltaje continuo: habitual en chips y microprocesadores. Son corrientes que no presentan alteraciones, el voltaje es constante.
Problema. Determinar la corriente resultante de una batería de 12V a un circuito con resistencia de 2, 2 



ELECTRODINÁMICA

La electrodinámica estudia fenómenos vinculados a la electricidad en movimiento.
La electrodinámica es la disciplina que se dedica a analizar los fenómenos que genera la electricidad cuando está en movimiento. Estos estudios se orientan a la interacción de campos magnéticos y eléctricos con cargas que se desplazan.
Antes de avanzar, cabe recordar que la electricidad es una fuerza que surge por la presencia de protones y electrones y se origina a partir del rechazo o la atracción entre partículas cargadas.


CORRIENTE ELÉCTRICA

Corrientes eléctricas en movimiento, cuando se unen mediante un conductor dos regiones que tienen diferente potencial eléctrico, las cargas eléctricas se mueven a través de dicho conductor y la corriente eléctrica queda establecida. La corriente consiste en el movimiento de iones positivos en un sentido y de iones negativos en el sentido opuesto. Una corriente eléctrica es decir por convención, el sentido de una corriente eléctrica es el sentido en que se mueven ( o moverían) las cargas eléctricas positivas.
Ejemplos: 
  1. Electrodomésticos: Los electrodomésticos como refrigeradores, hornos y lavadoras funcionan gracias a la corriente eléctrica.
  2. Carga de dispositivos electrónicos: Los cargadores de teléfonos móviles y computadoras portátiles utilizan corriente eléctrica para cargar las baterías.
  3. Transporte eléctrico: Vehículos eléctricos como automóviles, bicicletas y scooters utilizan corriente eléctrica para propulsarse.
  4. Sistemas de comunicación: Teléfonos, computadoras y televisores transmiten y reciben señales mediante corriente eléctrica
Problema. Por la sección transversal de un alambre pasan 10 coulombios en 4seg. ¿Calcular la intensidad de la corriente eléctrica?  
 
q = 10 coulombios           t = 4 seg.          i = ?

Problema. En los extremos de un conductor hay una diferencia de potencial de 20 voltios cuando lo atraviesa una corriente de 4 amp. ¿Calcular su resistencia ? 
 
V = 20 Voltios        i = 4 amp.      R = ?

Tipos de corriente eléctrica
  1. Corriente de conducción. Movimiento de cargas eléctricas libres (positivas o negativas)
  2. Corriente de convección. Movimiento de cuerpos cargados eléctricamente.
  3. Corriente de polarización. Movimiento de cargas eléctricas que se produce durante el periodo de polarización.
  • Corriente continua. 
Las cargas eléctricas fluyen siempre en el mismo sentido.
La gráfica que representa a una corriente eléctrica continua y constante.
  • Corriente alterna.
Las cargas eléctricas se desplazan primero en un sentido y luego en el sentido opuesto, a través del circuito.
La corriente alterna se representa por la gráfica.
Efectos de la corriente eléctrica.
  • Efecto térmico, la temperatura del medio (conductor) se eleva comunicando calor a sus alrededores.
  • Efecto magnético, el medio (conductor) se rodea de un campo magnético que puede afectar a otras corrientes.
  • Efecto químico, al atravesar ciertas sustancias, la corriente eléctrica las descompone químicamente.
  • Efecto luminoso, la corriente puede hacer que un material emite luz.
Intensidad de corriente eléctrica.
Se designa por I; es la cantidad de cargas eléctricas que pasa por el área transversal del conductor en la  unidad de tiempo.
Fórmula: F=I=q/t
  • I= intensidad de corriente eléctrica
  • q=carga eléctrica
  • t=tiempo
Si la sección transversal de un conductor existe una corriente eléctrica IA significa que por dicha sección está circulando una carga eléctrica de 1C en cada lapso de 1s
1A=1C/1s



CIRCUITO ELÉCTRICO

Componente esencial en cada sistema eléctrico o electrónico. Su función es convertir la tensión alterna en una tensión continua y lo más estable posible. 
  1. Transformador de entrada: Convierte la tensión de la red eléctrica en una tensión adecuada para el circuito.
  2. Rectificador a diodos: Transforma la corriente alterna en corriente continua.
  3. Filtro para el rizado: Suaviza la corriente continua eliminando fluctuaciones no deseadas.
  4. Regulador (o estabilizador) lineal: Asegura que la tensión de salida sea constante


Generadores

Los generadores en un circuito eléctrico son dispositivos que convierten otras formas de energía en energía eléctrica. Generalmente, la energía se produce mediante la inducción electromagnética, donde un conductor se mueve a través de un campo magnético o un campo magnético cambia dentro de un conductor, lo que genera corriente eléctrica. Aquí tienes una descripción de algunos tipos comunes de generadores:
Generadores de corriente continua (DC): Estos generadores producen corriente eléctrica que fluye siempre en la misma dirección.
Generadores de corriente alterna (AC): Estos generadores producen corriente eléctrica que cambia de dirección periódicamente. 
Generadores de turbina de vapor: Estos generadores utilizan vapor de agua para hacer girar una turbina, que a su vez hace girar un generador para producir electricidad.
Generadores de energía eólica: Estos generadores utilizan la energía cinética del viento para hacer girar las aspas de un rotor, que a su vez hace girar un generador para producir electricidad. 
Generadores de energía hidroeléctrica: Estos generadores utilizan la energía cinética del agua en movimiento (como la de los ríos o presas) para hacer girar una turbina, que a su vez hace girar un generador para producir electricidad.



CONDUCTORES

Los conductores en un circuito eléctrico son materiales que permiten que la corriente eléctrica fluya a través de ellos. Se utilizan para conectar diferentes componentes del circuito y transportar la electricidad desde la fuente de alimentación hasta los receptores o dispositivos que realizan alguna función. Aquí tienes información sobre los conductores más comunes:
Cables eléctricos: Son los conductores más utilizados en los circuitos eléctricos. Consisten en un núcleo conductor hecho de cobre o aluminio rodeado por un aislante para proporcionar protección y seguridad. 
Cables de cobre: El cobre es uno de los materiales conductores más comunes en la industria eléctrica debido a su alta conductividad eléctrica y su capacidad para formar cables flexibles y duraderos.
Cables de aluminio: Tienen una conductividad ligeramente menor que el cobre, pero son más ligeros y menos costosos.



RECEPTORES

Los receptores en un circuito eléctrico son dispositivos que convierten la energía eléctrica en otra forma de energía útil, como luz, movimiento, calor, sonido, etc. Estos dispositivos son los que aprovechan la electricidad para realizar una función específica. 
Bombillas (lámparas): Son dispositivos que convierten la energía eléctrica en luz visible.
Motores eléctricos: Son dispositivos que convierten la energía eléctrica en movimiento mecánico.
Calentadores eléctricos: Son dispositivos que convierten la energía eléctrica en calor. 



Elementos de protección


Los elementos de protección en un circuito eléctrico son dispositivos diseñados para salvaguardar tanto el equipo eléctrico como a las personas que interactúan con él. Aquí hay algunos elementos comunes de protección en un circuito eléctrico:
Interruptores de circuito (breakers): Son dispositivos automáticos de protección que cortan el suministro eléctrico cuando detectan una corriente excesiva, evitando así daños en el circuito y posibles riesgos de incendio o electrocución.
Fusibles: Funcionan de manera similar a los interruptores de circuito, pero en lugar de abrir o cerrar un contacto, el fusible se funde cuando hay una corriente excesiva, interrumpiendo el flujo de electricidad y protegiendo el circuito.
Relés térmicos: Son dispositivos de protección contra sobrecargas que se activan cuando la corriente eléctrica supera un valor predeterminado durante un tiempo prolongado.
Diferenciales (interruptores de falla a tierra): Detectan corrientes de fuga hacia tierra, como las que ocurren cuando una persona entra en contacto con un conductor eléctrico. 



Elementos de control

Los elementos de control en un circuito eléctrico son componentes diseñados para regular, supervisar o dirigir el flujo de corriente eléctrica. Aquí hay algunos elementos comunes de control en un circuito eléctrico:
Interruptores: Son dispositivos que abren o cierran un circuito eléctrico, permitiendo o interrumpiendo el flujo de corriente eléctrica. Pueden ser manuales o automáticos.
Controles de velocidad: En circuitos que alimentan motores eléctricos, los controles de velocidad regulan la velocidad de rotación del motor ajustando la cantidad de corriente eléctrica suministrada.
Relés de control: Son dispositivos electromagnéticos que controlan la operación de otros dispositivos eléctricos en el circuito.
Temporizadores: Controlan la duración de una operación eléctrica, permitiendo que ciertas acciones ocurran durante un período de tiempo específico antes de activar o desactivar un dispositivo.
Termostatos: Controlan la temperatura en un sistema eléctrico, activando o desactivando dispositivos de calefacción o refrigeración según sea necesario para mantener una temperatura específica.



CIRCUITO SIMPLE

Un circuito eléctrico consiste en cierto número de ramas unidas entre sí, de modo que al menos una de ellas cierre la trayectoria que se proporciona a la corriente. 

El circuito más sencillo consta de una sola fuente de fem unida a una sola resistencia. Si  representa la fem y R indica la resistencia total, la ley de ohm queda de la siguiente manera:  = IR Donde I es la corriente que circula por el circuito.
Toda la energía que se gana mediante una carga que pasa a través de la fuente de fem se pierde debido al flujo a través de la resistencia. Si se considera la adición de ciertos elementos al circuito, se dice que dos o más elementos están en serie si tienen un solo punto en común que no está conectado a un tercer elemento.
Para aplicar la ley de ohm de forma adecuada en un circuito con dos o más resistencias conectadas en serie es necesario calcular una resistencia equivalente, para esto se debe sumar el valor de cada una de las resistencias individuales


Fórmulas: 
Las fórmulas más básicas que se utilizan en un circuito simple son las leyes de Ohm, que relacionan la corriente eléctrica (I), el voltaje (V) y la resistencia (R) en un circuito:
Ley de Ohm: V = I * R
Donde 
  • V es el voltaje en voltios (V), I es la corriente en amperios (A) y R es la resistencia en ohmios (Ω).
  • Ley de Ohm para la resistencia: R = V / I
  • Esta fórmula se puede utilizar para calcular la resistencia en un circuito dado un voltaje y una corriente.
  • Ley de Ohm para la corriente: I = V / R
  • Esta fórmula se puede utilizar para calcular la corriente en un circuito dado un voltaje y una resistencia.


CIRCUITO EN SERIE

Se llama circuito en serie a un tipo de circuito eléctrico provisto de un único camino para la corriente, que debe alcanzar a todos los bornes o terminales conectados en la red de manera sucesiva, es decir uno detrás de otro, conectando sus puntos de salida con el de entrada del siguiente.

Fórmulas clave:
  • Resistencia equivalente: Req=R1+R2+R3...+Rn
Re =  es la resistencia total del circuito.
R1+R2+R3...+Rn = son las resistencias individuales de cada componente en serie.

  • Intensidad total: IT=I1=I2=I3...=In
IT = es la corriente total del circuito.
I1=I2=I3...=In = son las corrientes que pasan a través de cada componente en serie.

  • Voltaje final: Vf=V1+V2+V3...+Vn
Vf =  es el voltaje total suministrado al circuito.
V1+V2+V3...+Vn =   son los voltajes a través de cada componente en serie.

Problema. Tenemos tres resistencias en serie: R1 = 10 ohmios, R2 = 20 ohmios y R3 = 30 ohmios. Calcula la resistencia total del circuito.
Para resolver este ejercicio, sumamos las resistencias en serie: RT = R1 + R2 + R3 = 10 + 20 + 30 
Resultado. = 60 ohmios.

Problema. En un circuito en serie, la corriente es la misma en todos los componentes. Si tenemos una corriente de 2 amperios y una resistencia de 5 ohmios, ¿cuál es la caída de voltaje en el circuito?
Utilizando la ley de Ohm (V = I * R), podemos calcular la caída de voltaje: V = 2 * 5 
Resultado. = 10 voltios.

Problema. Tenemos un circuito en serie con una resistencia de 10 ohmios y una fuente de voltaje de 12 voltios. ¿Cuál es la corriente que fluye a través del circuito?
Usando la ley de Ohm nuevamente, podemos calcular la corriente: I = V / R = 12 / 10 
Resultado. = 1.2 amperios.


CIRCUITO EN PARALELO

Cuando hablamos de un circuito en paralelo o una conexión en paralelo, nos referimos a una conexión de dispositivos eléctricos (como bobinas, generadores, resistencias, condensadores, etc.) colocados de manera tal que tanto los terminales de entrada o bornes de cada uno, como sus terminales de salida, coincidan entre sí.


Fórmulas:

  • ΔVT= Voltaje total
  • ΔVrx= Voltajes 1, 2, 3 ... 
  • IT= Corriente total
  • Irx= Resistencia 1, 2, 3 …
  • RT= Resistencia total
  • Rx= Resistencia 1, 2, 3 ... 
Vídeo 1


LEY OHM

Ley en la electricidad que establece que: “la fuerza de una corriente continua es directamente proporcional a la diferencia de potencial e inversamente proporcional a la resistencia del circuito.”
fórmula de la ley de Ohm
Dónde:
  • R es la resistencia eléctrica. Por resistencia nos referimos al obstáculo que la corriente encuentra en su camino, cuanto más alto sea, más difícil será que la corriente lo atraviese. La unidad de medida de la resistencia son los ohmios, simbolizados por la letra griega omega (Ω).
  • I es la intensidad de una corriente eléctrica que atraviesa un conductor expersada en Amperios (A).
  • V es el voltaje. Por voltaje en cambio nos referimos a la diferencia de potencial entre un punto con respecto a otro expresado en Voltios (V).

Problema. Encontrar la corriente que circula por el circuito mostrado, suponiendo que se tiene una fuente de 12V.
Se puede resolver de dos formas, calculando la corriente que circula por cada resistencia y sumándole, o calculando la resistencia equivalente y obtener la corriente total. Se procederá a resolverlo por los dos métodos para demostrar que se obtienen los mismos resultados.

  • Método 1: calculando corrientes individuales

Paso 1: En un circuito paralelo el voltaje se mantiene constante entre cada división o rama, por lo que a partir del voltaje y resistencia se puede calcular la corriente que circula por cada rama mediante la ley de ohm.
Paso 2: Puesto que la corriente total es la suma de las corrientes individuales obtenemos la corriente que circula en el circuito: 
  • Método 2: calculando la resistencia total 
Paso 1: utilizando la suma de recíprocos calculamos la resistencia total.
Paso 2: Ahora utilizando la ley de Ohm calculamos la corriente total.
Como podemos observar de los dos métodos llegamos al mismo resultado.


POTENCIAL ELECTRICO 

La potencia eléctrica es la cantidad de energía eléctrica que se transfiere o consume por unidad de tiempo en un circuito eléctrico. Se mide en vatios (W), que es una unidad que representa un julio por segundo.
Matemáticamente, la potencia eléctrica ( P ) se puede calcular de varias maneras dependiendo de los valores conocidos del circuito:

1. Usando voltaje y corriente:
 P = V • I 
donde ( V ) es el voltaje (en voltios) y ( I ) es la corriente (en amperios).
2. Usando la ley de Ohm y la resistencia:
 P = I^2 • R 
donde  R  es la resistencia (en ohmios).
3. Usando el voltaje y la resistencia:
 P = V^2/R

Problema. Supongamos que tienes una bombilla que funciona con un voltaje de 120 voltios y consume una corriente de 0.5 amperios.
Queremos calcular la potencia eléctrica que consume la bombilla.
Usamos la fórmula de potencia eléctrica:
P = V. I
Sustituimos los valores conocidos:
P = 120 V × 0.5 A
P = 60W
Resultado. Entonces, la bombilla consume 60 vatios de potencia eléctrica. Esto significa que, cada segundo, la bombilla utiliza 60 julios de energía eléctrica para funcionar.


EFECTO JOULE

Transformación de la energía eléctrica en calor, que tiene lugar cuando una corriente eléctrica atraviesa un conductor.
Este efecto está presente siempre que se enciende cualquier aparato o dispositivo que necesite electricidad para funcionar.
Fórmula. 
Q = R·I2·t

  • Q = representa a la energía o calor desprendido (también puede verse representada en algunas fórmulas por la letra E de energy). Esta energía se mide normalmente en Julios aunque también puede ser en calorías.
  • R = Resistencia que opone un material al paso de los electrones.
  • I = Intensidad de corriente que se mide en Amperios y es la cantidad de corriente que circula por el circuito.
  • t = El Tiempo transcurrido que es medido en segundos.
Problema. Un radiador indica que posee una potencia de 2000W y está conectado a la toma de 220 V. Calcular lo siguiente: Intensidad de la corriente que circula por el radiador

Dato: el calor específico del agua es Ce = 4180 J/kg.K

Solución a
La potencia se define como energía por unidad de tiempo. Si en la ecuación dada al comienzo pasamos el factor Δt a la derecha, se tendrá precisamente energía por unidad de tiempo:

Q = I2.R. Δt → P = Q/ Δt = I2. R

La resistencia del elemento calefactor se puede conocer a través de la ley de Ohm: V = I.R, de la cual se deduce que I = V/R. por lo tanto:

P = I2. (V/I) = I. V

Así la corriente resulta:

I = P/ V = 2000 W / 220 V 
Resultado. = 9.09 A.


LEYES DE KIRCHHOFF

Aplicar el principio de conservación de la carga eléctrica y el principio de conservación de la energía a los circuitos eléctricos, con la finalidad de resolver los que tienen varias mallas.
  • Primera ley de Kirchoff
Es conocida también como ley de las corrientes o regla de los nodos, y establece que:
La suma de las corrientes que entra a un nodo es igual a la suma de las corrientes que salen de él.
∑ I = 0
Donde el símbolo Σ indica una sumatoria.
  • Segunda ley de Kirchoff
La suma algebraica de las caídas de tensión a lo largo de una malla es igual a 0.
Esta es una forma de aplicar la conservación de la energía en el circuito, ya que el voltaje en cada elemento es el cambio de energía por unidad de carga.
Por lo tanto, al recorrer una porción cerrada (una malla), la suma algebraica de las subidas y caídas de tensión es 0 y se puede escribir:
∑ V = 0

Solución de circuitos directos.

Un circuito de corriente directa comprende una serie de elementos tales como resistencias, condensadores y otros, conectados mediante alambres conductores y alimentados con una fuente de voltaje directo. Hay símbolos específicos para cada uno de estos elementos, por ejemplo, las fuentes de voltaje directo, que suministran corriente dc se simbolizan mediante dos líneas paralelas de distinta longitud o bien un círculo con el símbolo de la igualdad en su interior.
  1. Leyes de Kirchhoff
  2. Método del voltaje en los nodos
  3. Método de la corriente de malla

Solución de circuitos complejos.

  1. Método de análisis nodal: Analiza los nodos del circuito.
  2. Método de análisis de malla: Examina las mallas del circuito.
  3. Método de superposición: Considera cada fuente de energía por separado.
  4. Método de Thevenin y Norton: Simplifica el circuito utilizando equivalentes de Thevenin o Norton.


MÉTODO DE ANÁLISI NODAL

El método de análisis nodal es un método teórico para encontrar magnitudes eléctricas a través de analizar el circuito con el mismo número de nodos (incluyendo el nodo de referencia) con el mismo número de mallas en el circuito.

Método:
  1. Asignar voltajes en cada nodo con al menos 3 elementos, omitiendo el nodo de referencia.
  2. Aplicar trayectorias de corrientes saliendo de cada noto. Mantener iguales las trayectorias de las fuentes.
  3. Aplicar ley de corrientes de Kirchhoff en cada nodo, expresando las corrientes en función de voltajes y resistencias.
  4. Hacer un sistema de ecuaciones.
  5. Resolver el sistema.
  6. Restar los voltajes de nodos en cada componente compartido para encontrar los voltajes faltantes.


MÉTODO DE ANÁLISIS MALLA

Resolver circuitos eléctricos planos. 

Pasos.
  1. Aislar los bucles (mallas) en el circuito.
  2. Identificar las cargas de voltaje opuestas en cada malla.
  3. Sustituir los valores conocidos en las ecuaciones de las mallas para resolver las corrientes desconocidas.


MÉTODO DE SUPERPOSICIÓN

Análisis de circuitos eléctricos lineales y bilaterales con múltiples fuentes independientes.

Pasos.
  1. Considera cada fuente de voltaje independiente por separado. Apaga todas las demás fuentes o sustitúyelas con un cortocircuito.
  2. Si la fuente es de corriente, abre el circuito.
  3. Las resistencias internas de las fuentes deben permanecer en su lugar.


MÉTODO DE THÉVENIN Y NORTON

Simplificar el análisis de circuitos más complejos en un circuito equivalente simple, por medio de la sustitución de una fuente y una resistencia.
Se aplica a circuitos eléctricos, establece que un circuito lineal con dos terminales a y b, se puede reemplazar por otro completamente equivalente, que consta de una fuente de corriente llamada INo conectada en paralelo con una resistencia RNo. Vídeo Método y solución









FUENTES DE CONSULTA Y MATERIAL DE APOYO:

Material proporcionado por el docente. 


FUENTES DEL LIBRO CONSULTADO: 
  • Braun Eliezer, Electromagnetismo: de la ciencia a la tecnología, La ciencia
  • desde México/42, FCE, México, 1992.
  • Bueche, Frederick y Jerde, David, Fundamentos de física, t. II, McGraw-Hill,
  • México, 1996.
  • Cutnell, John y Jhonson, Kenneth, Física, Limusa-Noriega Editores, México,
  • 1999.
  • Gutiérrez, Calor, electromagnetismo y óptica, Limusa-Conalep, México,
  • 1999.
  • Gutiérrez A. Carlos y Gutiérrez, G.C., Practicas de física 2, Edición
  • Larousse, México, 2006.
  • Noreña, Francisco, Física de emergencia, Pangea, México, 1995.
  • Rius, Magdalena, et al., Calor y movimiento, La ciencia desde México/85,
  • FCE, México, 1992.
  • Sears, Francis, et al., Física universitaria, vol. 2, Pearson Educación,
  • México, 2004.
  • Taqueña, Julia y Martina, Esteban, De la brújula al spin. El magnetismo. La
  • ciencia para todos/56, FCE, México, 1997.
  • Tippens, Paul, Física. Conceptos y aplicaciones, McGraw-Hill, México,
  • 1989.

Comentarios

Publicar un comentario

Entradas populares de este blog

INICIO

 ENTORNO DE CULTURA DE PAZ Y NO VIOLENCIA Este contiene cada uno de los contenidos de las materias del proyecto transversal, el cual nosotros le llamamos: "MI ESPACIO VIRTUAL COMO ENTORNO DE APRENDIZAJE" En el cual, participan las materias: Biología II - Biol. Ámbar Pirrón Ponce Comunidades Virtuales - Ma. de Lourdes Bartolo Pérez Literatura II - Alejandra del Moral Aquino Mantenimiento de redes de cómputo - José Agustín Gutiérrez Bautista  Física II - Arq. Jesús Enrique Osorio Hernández Matemáticas IV - Ing. Silvestre Rojas Hernández
Leer más